等差數列原來如此重要
在近年來的公職類考試數量關系中，計算問題備受出題老師青睞，在考試中的占比也在不斷提升，而在計算問題眾多的考查題型中，等差數列作為相對而言比較重要的一個知識點應該引起我們足夠的重視，接下來浙江公務員考試網就帶大家一起來看一下等差數列。
了解更公務員考試信息
相關文章
一、定義和概念
等差數列：一個數列從第二項起，每一項與它的前一項的差等于同一個常數。
比如，數列1，3，5，7，9，11，在這個數列當中，后一項與前一項的差均為2，所以這是一個公差為2的等差數列。
首項：數列當中的第一項，用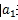
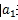表示。
表示。 末項：數列當中的最后一項，用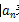
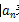表示。
表示。 公差：固定的差值，用d表示。
前n項和：用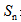
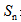表示。
表示。 二、基本公式
1.通項公式：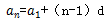
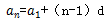
2.求和公式：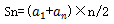
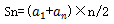
中項求和公式：
三、典型例題
某學校組織活動進行隊列訓練，學生們組成一個25排的隊列，后一排均比前一排多4個學生，最后一排有125個學生。則這個隊列一共有( )個學生。
A.1925 B.1875 C.2010 D.1765
【答案】A。解析：根據題目信息后一排均比前一排多4個學生，可以判斷這個隊列為公差為4的等差數列，其中n=25，d=4，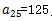
，問題所求為這個數列的前25項和。
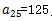，問題所求為這個數列的前25項和。 方法一：根據通項公式，求出第一項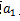
，
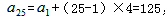，解得
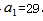。根據等差數列前n項和公式
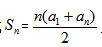，可得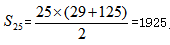
，共有1925個學生。選A。
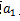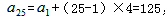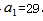，，解得。根據等差數列前n項和公式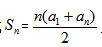，可得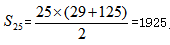，共有1925個學生。選A。方法二：直接求中間項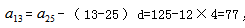
，則等差數列和為
。
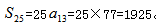通過例題的講解，相信大家已經對等差數列的相關知識點有了一定的了解，等差數列作為計算問題中比較重要的一個知識點需要各位同學重點掌握，相信各位同學經過不斷的練習和總結一定能夠很好的解決這部分題型。
可添加二維碼
微信公眾號 : zjgwyworg
（掃碼關注）
點擊分享此信息：
相關文章
